The Geometry of Big-Data Clouds
Clouds remain one of the largest puzzles in climate science. A new generation of climate models promises to enable fundamental new insights into how clouds couple with the circulation and shape climate change.
However, these new models also pose challenges in terms of their unstructured grids and the amount of data they produce. Thus, we, Petra Schwer and Aiko Voigt, have joined forces to apply methods from pure mathematics for the analysis of cloud structures simulated by the new unified ICON climate model system. With the help of the YIN Grant and two student assistants, we have
managed to develop a first prototype for identifying three-dimensional cloud structures on the native triangular grid of ICON.
Aiko (now Professor for Climate Science at the University of Vienna) is a climate dynamicist and modeler. In his BMBF-funded young investigator group at KIT, he has applied new storm-resolving simulations to study clouds. In contrast to tradi- tional climate models that use structured latitude-longitude grids with resolutions of around 100 km, these models use unstructured grids with much finer resolutions. For the employed ICON model, it was a triangular grid with a resolution as fine as 2 km. In addition to the massive increase in model data, the unstructured nature of the triangular grid challenges the analysis of coherent cloud structures and their geometrical properties. Established tools for connected component labeling on structured latitude-longitude grids can no longer be applied.
This is exactly where Petra has come in. A former junior professor at KIT, she is now Professor for Geometry at Otto von Guericke University of Magdeburg.
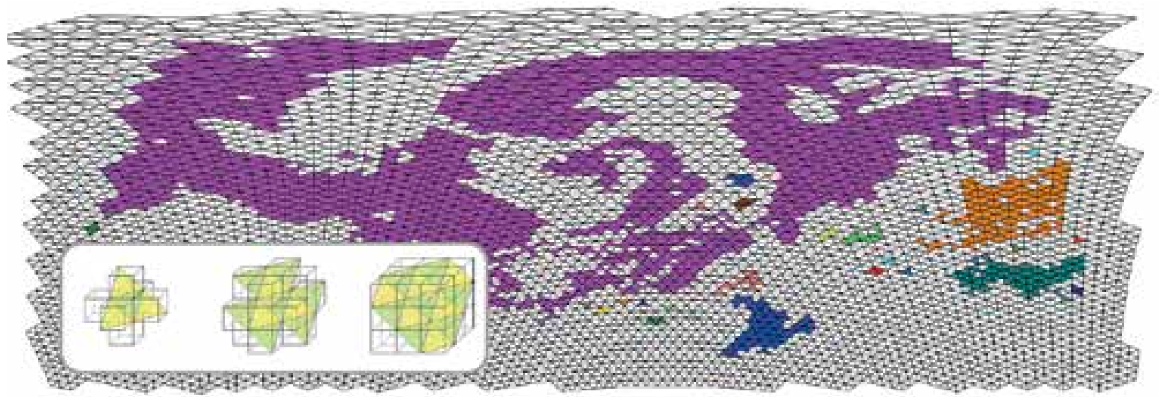
We started talking about the ICON model challenges during a YIN workshop on interdisciplinary collaboration in 2018. Soon, we realized that current methods from geometric group theory might provide a solution: A cubulation method turns complicated spaces with walls into com- plexes built entirely out of unit cubes. These are easier to study, while still carrying a lot of the same information.
In our joint project, we have translated the question of determining connected components of clouds on the ICON grid to the question of finding connected components on a 3-dimensional structured grid, where one can use existing connected component labeling tools. With the support of two brilliant student assistants, Nicole Knopf and Noam von Rotberg, we first developed a method to identify two-dimensional cloud components from a simulation of a North Atlantic cyclone. We later extended the method to three dimensions. Thus, our prototype can for example be used to identify the coherent slanted cloud structure that is generated by the upward motion within a cyclone.
The project was further supported by later funding from the KIT Center MathSEE: Mathematics in Sciences, Engineering, and Economics. A scientific publication on the method and the software is currently in preparation. We have also made initial contact with colleagues from other geoscience disciplines that might benefit from our approach.

